Exercícios de Números Complexos - Resolvidos
Caro estudante,
Selecionamos uma lista de exercícios sobre o conjunto dos números complexos para você que se prepara para concursos públicos ou carreiras militares deste ano.
Recomendo reservar um tempo para resolver todos eles e depois conferir o gabarito com a resolução comentada. Os exercícios sobre números complexos abordam:
>>> Soma, produto e divisão de números complexos;
>>> Potenciação e radiciação com números complexos;
>>> O plano de Argand-Gauss;
>>> Fórmula de Moivre;
>>> Forma trigonométrica ou polar de um número complexo;
>>> Módulo e Argumento de um número complexo;
>>> Raízes Complexas em equações polinomiais.
Desejo sucesso nos estudos e espero que estas questões resolvidas sobre o conjunto dos números complexos te ajudem em sua jornada.
1 - (ESA 2014) O número complexo i102, onde i representa a unidade imaginária,
A) é positivo.
B) é imaginário puro.
C) é real.
D) está na forma trigonométrica.
E) está na forma algébrica.
[A] duas raízes iguais a i, uma raiz racional e duas raízes irracionais.
[B] i e -i como raízes complexas e três raízes irracionais.
[C] uma raiz complexa i e quatro raízes reais.
[D] i e -i como raízes complexas e três raízes inteiras.
[E] três raízes simples e uma raiz dupla.
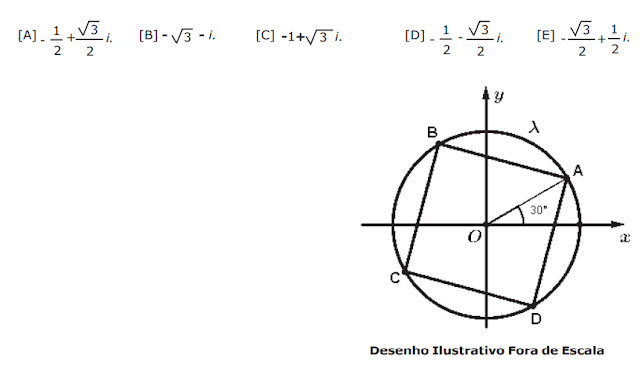
5 - (EsPCEx - 2018) No plano complexo, temos uma circunferência λ de raio 2 centrada na origem. Sendo ABCD um quadrado inscrito à λ , de acordo com a figura abaixo, podemos afirmar que o número complexo que representa o vértice B é
Link para a solução desta questão
Selecionamos uma lista de exercícios sobre o conjunto dos números complexos para você que se prepara para concursos públicos ou carreiras militares deste ano.
Recomendo reservar um tempo para resolver todos eles e depois conferir o gabarito com a resolução comentada. Os exercícios sobre números complexos abordam:
>>> Soma, produto e divisão de números complexos;
>>> Potenciação e radiciação com números complexos;
>>> O plano de Argand-Gauss;
>>> Fórmula de Moivre;
>>> Forma trigonométrica ou polar de um número complexo;
>>> Módulo e Argumento de um número complexo;
>>> Raízes Complexas em equações polinomiais.
Desejo sucesso nos estudos e espero que estas questões resolvidas sobre o conjunto dos números complexos te ajudem em sua jornada.
1 - (ESA 2014) O número complexo i102, onde i representa a unidade imaginária,
A) é positivo.
B) é imaginário puro.
C) é real.
D) está na forma trigonométrica.
E) está na forma algébrica.
2 - (ESA 2013) Com relação aos números complexos Z1= 2 + i e Z2= 1- i , onde i é a unidade imaginária, é correto afirmar
a) Z1. Z2= - 3 + i
b) |Z1| = √2
c) |Z2| = √5
d) |Z1. Z2| = √10
e) |Z1 + Z2| = √3
Link para a solução desta questão
3 - (EsPCEx - 2017) Na figura abaixo, está representado o plano de Argand-Gauss com os afixos de 12 números complexos, identificados de A a L. Sabe-se que esses afixos dividem a circunferência em 12 partes iguais e que A=(1,0).
O polígono regular cujos vértices são os afixos de 4√E é
[A] BEHK.
[B] CFIL.
[C] ADGJ.
[D] BDHJ.
[E] CEIK.
Link para a solução desta questão
4 - (EsPCEx - 2018) Sabendo que o número complexo i (sendo i a unidade imaginária) é raiz do polinômio p(x) = x5 - 2x4 - x + 2, podemos afirmar que p(x) tema) Z1. Z2= - 3 + i
b) |Z1| = √2
c) |Z2| = √5
d) |Z1. Z2| = √10
e) |Z1 + Z2| = √3
Link para a solução desta questão
3 - (EsPCEx - 2017) Na figura abaixo, está representado o plano de Argand-Gauss com os afixos de 12 números complexos, identificados de A a L. Sabe-se que esses afixos dividem a circunferência em 12 partes iguais e que A=(1,0).
O polígono regular cujos vértices são os afixos de 4√E é
[B] CFIL.
[C] ADGJ.
[D] BDHJ.
[E] CEIK.
Link para a solução desta questão
[A] duas raízes iguais a i, uma raiz racional e duas raízes irracionais.
[B] i e -i como raízes complexas e três raízes irracionais.
[C] uma raiz complexa i e quatro raízes reais.
[D] i e -i como raízes complexas e três raízes inteiras.
[E] três raízes simples e uma raiz dupla.
5 - (EsPCEx - 2018) No plano complexo, temos uma circunferência λ de raio 2 centrada na origem. Sendo ABCD um quadrado inscrito à λ , de acordo com a figura abaixo, podemos afirmar que o número complexo que representa o vértice B é
6 - (ESA 2019) Para que z = (5+i) / (a - 2i) seja um imaginário puro, o valor de a deve ser:
a) 2/5
b) -2/5
c) 0
d) 10
e) -10
7 - (EsPCEx 2020) Na figura abaixo está representado o plano de Argang-Gauss com os afixos de 12 números complexos. Sabe-se que esses afixos dividem a circunferência em 12 partes iguais e que Z0 =1.
Sobre o número complexo dado por [ (Z2)² . Z5 ] / Z3 é correto afirmar que é um número
[A] real e negativo.
[B] real e positivo.
[C] Imaginário com parte real negativa e parte imaginária positiva.
[D] Imaginário com parte real positiva e parte imaginária negativa.
[E] Imaginário puro com parte imaginária negativa.