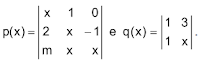Exercícios Resolvidos de Polinômios e Equações Polinomiais
Caro estudante,
Selecionamos uma lista de exercícios sobre polinômios, funções e equações polinomiais para você que se prepara para concursos públicos ou carreiras militares deste ano.
Recomendo reservar um tempo para resolver todos eles e depois conferir o gabarito com a resolução comentada. Desejo sucesso nos estudos e espero que estas questões resolvidas sobre polinômios te ajudem em sua jornada.
1 - (Vestibular CEDERJ 2019.2) Se m e n são números reais tais que o polinômio p(x) = x³ - x² + mx + n é divisível por x² + 1, então m - n é igual a
a) 0
b) 1
c) -2
d) 2
a) 1
b) 2
c) 3
d) 4
5 - (EsPCEx 2019) Se a equação polinomial x² +2x+8=0 tem raízes a e b e a equação x² +mx+n=0 tem raízes (a+1) e (b+1), então m+n é igual a
a) -2
b) -1
c) 4
d) 7
e) 8
Link para a solução desta questão
Selecionamos uma lista de exercícios sobre polinômios, funções e equações polinomiais para você que se prepara para concursos públicos ou carreiras militares deste ano.
Recomendo reservar um tempo para resolver todos eles e depois conferir o gabarito com a resolução comentada. Desejo sucesso nos estudos e espero que estas questões resolvidas sobre polinômios te ajudem em sua jornada.
1 - (Vestibular CEDERJ 2019.2) Se m e n são números reais tais que o polinômio p(x) = x³ - x² + mx + n é divisível por x² + 1, então m - n é igual a
a) 0
b) 1
c) -2
d) 2
2 - (EsPCEx 2019) Dividindo-se o polinômio P(x) = 2x4 - 5x3 + kx - 1 por (x-3) e (x+2), os restos são iguais. Neste caso, o valor de k é igual a
[A] 10. [B] 9. [C] 8. [D] 7. [E] 6.
Link para a solução desta questão
3 - (EsPCEx - 2018) Sabendo que o número complexo i (sendo i a unidade imaginária) é raiz do polinômio p(x) = x5 - 2x4 - x + 2, podemos afirmar que p(x) tem
[A] duas raízes iguais a i, uma raiz racional e duas raízes irracionais.
[B] i e -i como raízes complexas e três raízes irracionais.
[C] uma raiz complexa i e quatro raízes reais.
[D] i e -i como raízes complexas e três raízes inteiras.
[E] três raízes simples e uma raiz dupla.
Link para a solução desta questão
4 - (Concurso: Professor de Matemática - Rio das Ostras - RJ. Banca: IBAM. Ano: 2019) Dividindo-se o polinômio 2x³ + kx² - x - 7 por (2x-4), obtém-se resto 11. O valor de k é:[A] 10. [B] 9. [C] 8. [D] 7. [E] 6.
Link para a solução desta questão
3 - (EsPCEx - 2018) Sabendo que o número complexo i (sendo i a unidade imaginária) é raiz do polinômio p(x) = x5 - 2x4 - x + 2, podemos afirmar que p(x) tem
[A] duas raízes iguais a i, uma raiz racional e duas raízes irracionais.
[B] i e -i como raízes complexas e três raízes irracionais.
[C] uma raiz complexa i e quatro raízes reais.
[D] i e -i como raízes complexas e três raízes inteiras.
[E] três raízes simples e uma raiz dupla.
Link para a solução desta questão
a) 1
b) 2
c) 3
d) 4
5 - (EsPCEx 2019) Se a equação polinomial x² +2x+8=0 tem raízes a e b e a equação x² +mx+n=0 tem raízes (a+1) e (b+1), então m+n é igual a
a) -2
b) -1
c) 4
d) 7
e) 8
Link para a solução desta questão
6 - (UNICAMP - 2020) Seja a função polinomial do terceiro grau f(x) = x³ - x² - 2x + 1, definida para todo número real x. A figura abaixo exibe o gráfico de y=f(x), no plano cartesiano, em que os pontos 𝐴, 𝐵 e 𝐶 têm a mesma ordenada. A distância entre os pontos 𝐴 e 𝐶 é igual a
a) 2.
b) 2√2.
c) 3.
d) 3√2.
a) 2.
b) 2√2.
c) 3.
d) 3√2.
7 - (EsPCEx - 2019) Sabe-se que as raízes da equação x³-3x²-6x+k=0 estão em progressão aritmética. Então podemos afirmar que o valor de k/2 é igual a
8 - (EsPCEx 2020) Se o polinômio p(x)= x³ + ax² - 13x + 12 tem x=1 como uma de suas raízes, então é correto afirmar que
[A] x=1é raiz de multiplicidade 2.
[B] as outras raízes são complexas não reais.
[C] as outras raízes são negativas.
[D] a soma das raízes é igual a zero.
[E] apenas uma raiz não é quadrado perfeito.
| 9 - (Vunesp 2020) Considere os polinômios |
Para que p(x) seja divisível por q(x), é necessário que m seja igual a
(A) 30. (B) 12. (C) –12. (D) –3. (E) –30.
Link para a solução desta questão