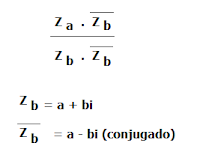(EsPCEx 2020) Na figura abaixo está representado o plano de Argang-Gauss com os afixos de 12 números complexos. Sabe-se que esses afixos dividem a circunferência em 12 partes iguais e que Z0 =1.
(EsPCEx 2020) Na figura abaixo está representado o plano de Argang-Gauss com os afixos de 12 números complexos. Sabe-se que esses afixos dividem a circunferência em 12 partes iguais e que Z0 =1.
Sobre o número complexo dado por [ (Z2)² . Z5 ] / Z3 é correto afirmar que é um número
[A] real e negativo.
[B] real e positivo.
[C] Imaginário com parte real negativa e parte imaginária positiva.
[D] Imaginário com parte real positiva e parte imaginária negativa.
[E] Imaginário puro com parte imaginária negativa.
>> Forma trigonométrica ou polar do número complexo
z = ρ (cosθ + i senθ)
>> Fórmula de Moivre para potenciação do número complexo.
zn = |z|n (cos nθ + i sen nθ)
Repare na figura do enunciado que o ângulo entre cada número complexo adjacente é de 30º. Isso porque a circunferência (360º) foi dividida em 12 partes, sendo assim 360º/12 = 30º.
Como Z0 = 1, então ρ = 1, que é próprio raio desta circunferência.
Vamos escrever Z2, Z3 e Z5 usando a forma polar.
Z2 = 1 (cos 60º + i sen 60º) = 1/2 + [(√3)/2] i
Z3 = 1 (cos 90º + i sen 60º) = i
Z5 = 1 (cos 150º + i sen 150º) = - [(√3)/2] + (1/2) i
Vamos agora usar a fórmula de Moivre para obter Z². Um detalhe é que nós podemos obter Z² fazendo simplesmente o produto Z x Z, uma vez que essa potência é de um grau baixo. Caso o expoente fosse maior, por exemplo, Z9 , então ficaria impraticável fazer ZxZxZ ... x Z por 9 vezes. Portanto, para fins de estudo, vamos resolver essa questão usando a fórmula de Moivre:
z2 = |1|2 (cos 2x60º + i sen 2x60º)
z2 = 1 (cos 120º + i sen120º)
z² = -1/2 + [(√3)/2]i
Vamos calcular Z² . Z5 . Neste produto, basta multiplicar todos os elementos do primeiro número complexo por todos os elementos dos segundo.
[ -1/2 + [(√3)/2]i ] . [ - [(√3)/2] + (1/2) i ]
+ (√3)/4 - (1/4) i - (3/4)i + [(√3)/4] i²
+ (√3)/4 - (4/4) i - [(√3)/4] = -i
Por último, basta dividir -i / i = -1 [Alternativa correta é a letra A]
Curiosidade: esta divisão de números complexos foi mais simples, pois ambos só possuem parte imaginária, caso a divisão fosse feita entre números complexos com parte real e imaginária, então teríamos que usar a fórmula da divisão de dois números complexos za / zb:
Curiosidade 2: podemos usar esta fórmula para dividir -i por i. O conjugado do denominador (i) é igual a (-i).
= -i . (-i) /i . (-i)
= + i² / - i²
= + ( -1) / - (-1)
= -1 / + 1 = -1
Aproveite e confira mais exercícios resolvidos de números complexos.
>> Exercícios de Números Complexos - Resolvidos
Um forte abraço e bons estudos.