(IME 2020) Seja 𝐴 = { 𝑧 ∈ 𝐶 | 2 ≤ |𝑧 − 3 − 4𝑖| ≤ 3} onde 𝐶 é o conjunto dos números complexos. O valor do produto entre o simétrico do complexo de menor módulo do conjunto 𝐴 e o conjugado do complexo de maior módulo do mesmo conjunto 𝐴 é:

(IME 2020) Seja 𝐴 = { 𝑧 ∈ 𝐶 | 2 ≤ |𝑧 − 3 − 4𝑖| ≤ 3} onde 𝐶 é o conjunto dos números complexos. O valor do produto entre o simétrico do complexo de menor módulo do conjunto 𝐴 e o conjugado do complexo de maior módulo do mesmo conjunto 𝐴 é: 

(A) -16 (B) -8 (C) -16/5 (D) 1 (E) 16

Solução: questão sobre números complexos do IME (prova de 2019/2020) , nesta resolução, vamos usar x como a parte real do número complexo e y a parte imaginária, sendo assim, os números complexos do conjunto A terão a forma: z = x + yi , respeitando o limite a seguir:

2 ≤ | x + yi - 3 - 4𝑖 | ≤ 3

2 ≤ | (x − 3) + (y − 4) 𝑖 | ≤ 3

O módulo de um número complexo z = a + b.i  é dado por  √(a² + b²).

2  ≤    √ [(x-3)² + (y-4)² ]    ≤  3

√ [(x-3)² + (y-4)² ]  ≥  2      e      √ [(x-3)² + (y-4)² ]  ≤  3

(x-3)² + (y-4)²   ≥  2²           e      (x-3)² + (y-4)²   ≤  3²

No plano complexo, o conjunto A está limitado por essas duas equações de circunferência.  Vamos representá-las no plano de Argand-Gauss.

Agora precisamos encontrar, dentro desse conjunto, dois números complexos,  o que possui o menor módulo e também aquele que possui o maior módulo, para isso traçaremos uma reta que passa pela origem e pelo ponto (3,4) que é o centro das circunferências concêntricas.

A equação de reta é facilmente obtida, pois passa pela origem e pelo ponto (3,4), logo tem coeficiente angular 4/3.  A reta tem equação y = (4/3)x.

O número complexo de menor e o de maior módulo estão sobre a circunferência de raio igual a 3.  Sendo assim vamos aplicar em:  (x-3)² + (y-4)² = 3²   o valor de y = (4/3)x.

x² - 6x + [(4/3)x]² - 8 [ (4/3)x ] + 16 = 0

25 x² - 150 x + 144 = 0

Resolvendo esta equação do segundo grau pelo método de Bhaskara, chegaremos a x1 = 6/5 e x2 = 24/5.

y1 = (4/3) . x1 = (4/3) . (6/5) =  8/5

y2 = (4/3) . x2 = (4/3) . (24/5) = 32/5 

Complexo de menor módulo: 6/5 + (8/5) i

Complexo de maior módulo: 24/5 + (32/5) i

Simétrico do complexo de menor módulo:  - 6/5 - (8/5) i

Conjugado do complexo de maior módulo:  24/5 - (32/5) i

[ - 6/5 - (8/5) i ] x [ 24/5 - (32/5) i ]

- 144/25  + (192/25) i - (192/25) i + (256 /25) i²

- 144/25 - 256 / 25

- 400 / 25

-16 

Alternativa correta é a letra a). 

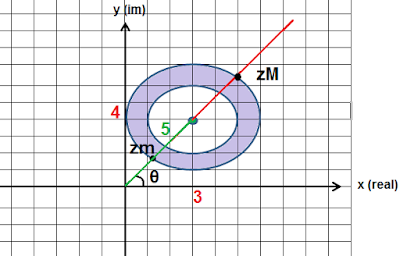
Curiosidade: também podemos obter os números complexos zm e zM por meio de sua forma polar ou trigonométrica [ z = |z| (cosθ + i sen θ) ]. Vamos analisar a figura a seguir: Repare que o módulo de zM é 5 + 3 = 8. Já o módulo de zm é 5 - 3 = 2. zM = |zM| . (cosθ + i . senθ) = 8 . (3/5) + 8 . (4/5)i = 24/5 + (32/5) i  zm = |zm| . (cosθ + i . senθ) = 2 . (3/5) + 2 . (4/5)i = 6/5 + (8/5) i

Aproveite e continue praticando com uma Lista de Exercícios de Números Complexos - Resolvidos.

Um forte abraço e bons estudos.