(IME 2020) Seja U o conjunto dos 1000 primeiros números naturais maiores que zero. Considere que zeros à esquerda são omitidos. Seja A ⊆ U o conjunto de números cuja representação na base 10 tem o algarismo mais significativo igual a 1; e B ⊆ U o conjunto de números cuja representação na base 4 tem o algarismo mais significativo igual a 2. As cardinalidades de A - B e de B - A são, respectivamente: 

(A) 46 e 277 (B) 45 e 275 (C) 44 e 275 (D) 45 e 277 (E) 46 e 275

Observação: 

• cardinalidade de um conjunto finito é o número de elementos distintos desse conjunto.

Solução:  questão de teoria dos conjuntos do exame do IME 2019/2020 que envolve também a mudança de base de números naturais.

A = {1 ; 10, ......, 19 ; 100, ......,  199 ; 1000 }

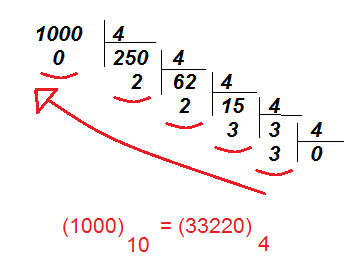
Para formarmos o conjunto B, primeiramente vamos converter 1000 que está na base 10 para a base 4, utilizando o método das divisões sucessivas.

Temos que os elementos do conjunto B estão limitados entre (1)4 e (33220)4 , pois B ⊆ U. Os elementos do conjunto B ("conjunto de números cuja representação na base 4 tem o algarismo mais significativo igual a 2") são os elementos a seguir que estão na base 4:

2
20, 21, 22, 23
200, ......................,  233          [apoiador 300]
2000, ....................., 2333        [apoiador 3000]
20000, ..................., 23333      [apoiador 30000]


Precisamos levá-los para a base 10, para formarmos o conjunto B.   Para facilitar os cálculos "puxei" os números "apoiadores".  Por exemplo, ao invés de converter 233, vamos converter o seu apoiador que é 300 e depois subtraímos 1 unidade.  O 300 é o número uma unidade após o 233. Convertendo:

2
8, 9, 10, 11
2 x 4², ............, 3 x 4²   - 1    
2 x 4³ ,............, 3 x 4³   - 1    
2 x 44 ,............, 3 x 44   - 1    

Finalmente teremos o conjunto B escrito na base 10:

2
8, 9, 10, 11
32, ........ , 47
128, ........, 191
512, ........, 767

Para facilitar nossa visualização vamos escrever A e B aqui embaixo.

A = {1 ; 10, ......, 19 ; 100, ......,  199 ; 1000 }

B = { 2, 8, 9, 10, 11 ; 32, ....., 47 ; 128, ...., 191 ; 512, ...., 767 }

Calculando A - B:

A - B = { 1 ; 12, ..., 19; 100, ...., 127 ; 192, ..., 199 ; 1000}
Contando os elementos de (A-B) = 1 + 8 + 28 + 8 + 1 = 46 elementos

Calculando B - A:
B - A = {2, 8, 9 ; 32, ....., 47 ; 512, ...., 767 }
Contando os elementos de (B-A) = 3 + 16 + 256 = 275 elementos

Sendo assim, a alternativa correta é a letra (E) 46 e 275.

Aproveite e continue praticando com uma lista de questões anteriores do IME.

Um forte abraço e bons estudos.