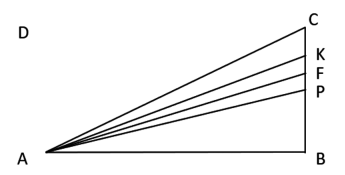
(PAES UEMA - 2021) Considere o triângulo retângulo ABC a seguir em que o comprimento do lado AB é o quádruplo do comprimento do lado BC e ainda que P seja o ponto médio de CB, K seja o ponto médio do segmento CP e F seja o ponto médio do segmento KP.


A tangente do ângulo FÂP é 

a) 1/8 b) 8/261 c) 5/32 d) 3/16 e) 8/131

Solução: questão de matemática do PAES (Processo Seletivo de Acesso à Educação Superior) para UEMA (Universidade Estadual do Maranhão). Prova aplicada no dia 05/07/2021.

Ilustrando a figura com as informações do enunciado, temos a seguinte estrutura: 



Nosso objetivo é encontrar a tangente do ângulo FÂP que está representado pelo ângulo a.  Podemos encontrar o ângulo a usando a tg (a+b).  Sabemos que:

tg (a+b) = [ tg (a) + tg (b) ] / [ 1 - tg (a) . tg (b) ]

** Vamos calcular isoladamente os valores de tg (b) e o valor de tg (a+b) e aplicá-los na fórmula acima.  Fazendo isso, encontraremos tg(a).

Sabemos, das relações trigonométricas no triângulo retângulo, que a tangente de um ângulo é igual ao cateto oposto dividido pelo cateto adjacente, sendo assim:

tg (b) = (x/2) / (4x) 
tg (b) = (x/2) * (1/4x) 
tg (b) = (1/2) * (1/4) 
tg (b) = 1/8

tg (a+b) = (x/8 + x/2) / 4x
tg (a+b) = (5x/8) / 4x
tg (a+b) = (5x/8) * (1/4x)
tg (a+b) = (5/8) * (1/4)
tg (a+b) = 5/32

Agora, vamos aplicar estes valores na fórmula de tg(a+b)

tg (a+b) = [ tg (a) + tg (b) ] / [ 1 - tg (a) . tg (b) ]
5/32 = [ tg (a) + 1/8 ] / [ 1 - tg (a) . (1/8) ]
5/32 . [ 1 - tg (a) . (1/8) ] = tg (a) + 1/8
5/32  -  (5/32) . tg (a) . (1/8) =  tg (a) + 1/8
5/32 - 1/8  - (5/256) tg (a)  = tg (a)
5/32 - 4/32  = tg (a) + (5/256) . tg (a)
1/32 = (256/256) . tg (a) + (5/256) . tg (a)
1/32 = (261/256) . tg (a) 
tg (a)  = 256/(32 . 261)
tg (a)  = 8/261
  
Alternativa correta é a letra b).

Aproveite e continue praticando com uma lista de questões anteriores do PAES UEMA

Um forte abraço e bons estudos.