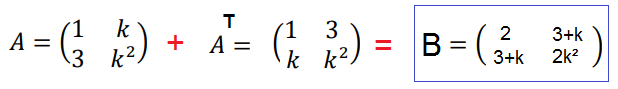(UNICAMP 2022) Considere a matriz

e seja 𝐵 = 𝐴 + 𝐴𝑇, onde 𝐴𝑇 é a transposta da matriz 𝐴. 

Sobre o sistema

é correto afirmar que:

a) se 𝑘 = 0, o sistema não tem solução.
b) se 𝑘 = −1, o sistema tem infinitas soluções.
c) se 𝑘 = −1, o sistema não tem solução.
d) se 𝑘 = 3, o sistema tem infinitas soluções.

Solução: questão de matemática do Vestibular UNICAMP 2022. Prova aplicada no dia 07/11/2021.

Primeiramente, vamos calcular 𝐴𝑇  e B.



Sobre os sistemas lineares, vamos relembrar o seguinte:

SPD - Sistema Possível e Determinado - "admite solução única"   (Δ ≠ 0)
SPI - Sistema Possível e Indeterminado - "admite infinitas soluções" (Δ = Δx = Δy = 0)
S.I. - Sistema Impossível - "não admite solução" (Δ=0 e pelo menos um deles Δx≠0 ou Δy ≠0)

Calculando Δ, que é o determinante da matriz dos coeficientes, ou seja, é o determinante da matriz B:

Δ = 4k² - (3+k)²
Δ = 4k² - (9 + 6k + k²)
Δ = 4k² - 9  - 6k - k²
Δ = 3k² - 6k - 9

As raízes de 3k² - 6k - 9 são k = -1 e k = 3.  Logo, 

>>> SPD   ( ocorrerá sempre que Δ ≠ 0, ou seja, quando k ≠ -1 ou k ≠ 3)

Já podemos julgar a alternativa (a), ela está errada, pois quando k=0 o sistema será SPD.

O próximo passo é analisar o que acontece quando k = -1, já sabemos que Δ valerá 0.  Agora precisamos analisar Δx e Δy.


Repare que quando k = -1, o valor de Δ = 0 e os valores de Δx e Δy são diferentes de 0.  Isto quer dizer que o sistema será impossível.  

Repare bem como ficou o sistema:

2x + 2y = 2021
2x + 2y = 2022   (impossível) 
 
Alternativa correta é a letra c).

Como exercício, você pode julgar também a letra (d) e perceberá que quando k =3 o sistema também será um SI.

Aproveite e continue praticando com uma lista de questões anteriores da UNICAMP.

Um forte abraço e bons estudos.