(ENEM 2021) O instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura 1.


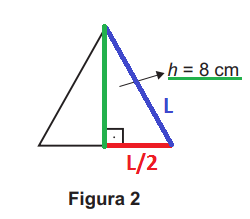
Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo.  A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2.  Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura.  Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.

Considere 1,7 como valor aproximado para √3.

Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é

a) 9,07.
b) 13,60.
c) 20,40.
d) 27,18.
e) 36,24.

Solução: questão de matemática do ENEM 2021,  prova aplicada no dia 28/11/2021.

O objetivo da questão é encontrar o comprimento da barra, ou seja, o perímetro do triângulo equilátero de lado (L) e altura h = 8 cm.  Podemos encontrar o lado (L) aplicando o Teorema de Pitágoras no triângulo retângulo a seguir:

Ou aplicar direto a fórmula da altura do triângulo equilátero que vale h = (L√3)/2 .  Vamos por este caminho:

8 = (L√3)/2
16 = √3 . L
L = 16/√3  (vamos racionalizar multiplicando esta fração por √3/√3)
L = 16/√3 * √3/√3
L = (16√3)/3

Vamos deixar para fazer a conversão √3 ≅ 1,7 apenas no final.

Como o objetivo é encontrar o perímetro que é igual a L + L + L = 3L, então:

Perímetro =  3 .  (16√3)/3 = 16√3 ≅ 16 . 1,7  ≅ 27,2 cm.
 
Alternativa correta é a letra d).

Aproveite e continue praticando com uma lista de questões anteriores do ENEM.

Um forte abraço e bons estudos.