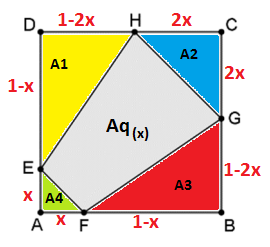
(FAMEMA 2022) A figura a seguir mostra um quadrado ABCD de lado 1, os pontos E, F, G, H pertencentes aos lados DA, AB, BC, CD, respectivamente, e o polígono EFGH.

Sabe-se que CG = CH = 2AE = 2AF. O valor máximo da área do polígono EFGH é de 

(A) 1/2. (B) 2/3. (C) 3/4. (D) 3/5. (E) 5/8.

Solução: questão de matemática do Vestibular da Faculdade de Medicina de Marília, ano: 2022, banca examinadora: FGV.  Prova aplicada no dia 05/12/2021.

Uma questão bem interessante sobre geometria plana (áreas de figuras planas), onde utilizaremos a maximização utilizando a fórmula das coordenadas do vértice de uma parábola.

Em primeiro lugar, vamos preencher a figura com informações importantes para nossa resolução.


Ilustramos a figura da seguinte forma:  atribuímos o valor de x para AE e AF. De acordo com o enunciado CG e GH terão que valer o dobro, ou seja 2x.  Como os lados do quadrado ABCD valem 1, então:
DH + HC = 1  (obtemos DH = 1-2x)
CG + GB = 1  (obtemos GB = 1-2x)
AF + FB  = 1  (obtemos FB = 1-x)
AE + ED = 1  (obtemos ED = 1-x) 

Com isso, obtivemos as medidas de todos os segmentos.

Agora, nosso objetivo é maximizar a área do quadrilátero EFGH em função de x, a qual chamamos simplesmente de Aq(x).  Perceba que Aq(x) = Área do quadrado ABCD - A1 - A2 - A3 - A4

Como o quadrado ABCD tem lado igual a 1, então sua área vale lado² = 1² = 1.

Aq(x) = 1 - A1 - A2 - A3 - A4

Vamos calcular as áreas A1, A2, A3 e A4.

A1 = (1-x)(1-2x)/2  = (1 -2x - x + 2x²)/2 
A1 = (1-3x+2x²)/2

A2 = (2x.2x)/2 = 4x²/2 
A2 = 2x²

A3 = A1 = (1-3x+2x²)/2
 
A4 = (x.x)/2 
A4 = x²/2

Voltamos a área do quadrilátero

Aq(x) = 1 - (1-3x+2x²)/2 - 2x² - (1-3x+2x²)/2 - x²/2
Aq(x) = 1 - 2.(1-3x+2x²)/2 -  5x²/2
Aq(x) = 1 - (1-3x+2x²) -  5x²/2
Aq(x) = 1 - 1 + 3x - 2x² - 5x²/2
Aq(x) = -9x²/2 + 3x 

Agora, nosso objetivo é maximizar essa função do segundo grau.  Esse tipo de exercício envolve as coordenadas do vértice da parábola.  Perceba que Aq(x) = -9x²/2 + 3x  tem o gráfico de uma função do segundo grau, ou seja, o gráfico de uma parábola e que possui concavidade voltada para baixo, isto porque seu coeficiente "a" é negativo (a = -9/2), então a parábola fica com um formato de ∩.  Portanto, esta parábola terá um ponto de máximo, exatamente sobre seu vértice. Veja na ilustração a seguir:

  fórmulas das coordenadas do vértice de uma parábola


As fórmulas das coordenadas do vértice da parábola (Xv,Yv) são:

Xv = -b/2a
Yv = -Δ/4a  onde   Δ = b² - 4ac

Nesta questão, nos interessa encontrar apenas o Yv, pois o requisito do enunciado é "O valor máximo da área do polígono EFGH ".

Δ = b² - 4ac
Δ = 3² - 4(-9/2)(0)
Δ = 9 - 0
Δ = 9

Yv = -Δ/4a
Yv = -9/[4 (-9/2)]
Yv = -9/[2 (-9)]
Yv = -9/-18
Yv = 1/2

Sendo assim, o valor máximo da área do polígono EFGH é de 1/2.
 
Alternativa correta é a letra a).

Aproveite e continue praticando com uma lista de questões anteriores da FAMEMA.

Um forte abraço e bons estudos.