(UERJ 2017) Dois cubos cujas arestas medem 2 cm são colados de modo a formar o paralelepípedo ABCDA’B’C’D’. Esse paralelepípedo é seccionado pelos planos ADEF e BCEF, que passam pelos pontos médios F e E das arestas A’B’ e C’D’, respectivamente. A parte desse paralelepípedo compreendida entre esses planos define o sólido ABCDEF, conforme indica a figura a seguir.
(A) 4
(B) 6
(C) 8
(D) 12
Solução: questão de matemática do Vestibular UERJ 2017, prova do dia 16/10/2016 (2° Exame de Qualificação).
Solução: questão de matemática do Vestibular UERJ 2017, prova do dia 16/10/2016 (2° Exame de Qualificação).
Repare que o sólido ABCDEF é um prisma de base triangular. Podemos calcular seu volume por meio da fórmula:
Volume = (área da base triangular) x (altura do prisma)
** Atenção para não confundir este sólido geométrico com uma pirâmide.
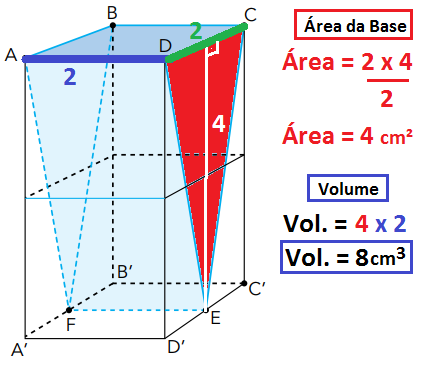
Vamos calcular a área da base triangular, tomando como referência o triângulo DCE. Perceba que este triângulo possui medida da base igual a 2 e altura igual a 4. Sendo assim, a área deste triângulo é igual a:
Área = (base x altura ) / 2
Área = (2 x 4) / 2
Área = 4 cm²
A altura do prisma é igual a medida do segmento AD = 2 cm. Finalmente, basta aplicar na fórmula do volume de um prisma de base triangular:
Volume = (área da base triangular) x (altura do prisma)
Volume = 4 x 2
Volume = 8 cm³
Alternativa correta é a letra c).
Veja a seguir uma ilustração dos cálculos da área da base triangular e do volume do prisma de base triangular.
Aproveite e continue praticando com uma lista de questões de matemática da UERJ.
Um forte abraço e bons estudos.