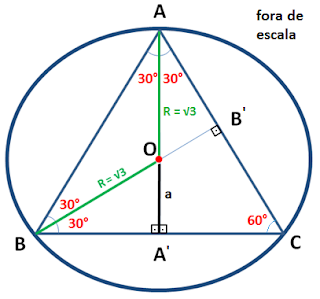
(SEEDUC-RJ 2014) A medida do apótema do triângulo equilátero inscrito em um círculo cujo raio mede √3 é igual a:
(Professor Docente I - Matemática - 2014 - Banca CEPERJ) A medida do apótema do triângulo equilátero inscrito em um círculo cujo raio mede √3 é igual a:
a) √3
b) 3
c) 6
d) 3/2
e) √3
2
Solução: questão do concurso para professor de matemática da Secretaria de Educação do Rio de Janeiro. Banca organizadora CEPERJ, 2014.
Vamos ilustrar a resolução deste problema, onde
R = raio do círculo = √3
a = apótema do triângulo equilátero (nosso objetivo)
Note que o apótema do triângulo equilátero é a medida (a) que parte do baricentro (ponto de encontro das medianas) do triângulo e alcança um de seus lados formando com este um ângulo de 90°.
Sabemos que no triângulo equilátero ABC a altura, mediana e bissetriz, referente a cada lado, estão sobre a mesma reta. Podemos perceber que o segmento AA' é a mediana referente ao lado BC. Na mediana, uma relação muito importante é a seguinte:
AO = 2 x OA'
Ou seja, na mediana, a distância do vértice até o baricentro é o dobro da distância do baricentro até o ponto médio do lado oposto. Isto quer dizer que
AO = 2 x OA'
√3 = 2 x a
a = (√3)/2
Alternativa correta é a letra e).
Uma outra forma de encontrarmos a, é por meio das relações trigonométricas no triângulo retângulo OBA'. Sabemos que o ângulo ABC vale 60° e que o ângulo OBA' vale a metade de ABC, ou seja, vale 30°.
Podemos visualizar, no triângulo retângulo BOA', que
seno 30° = cateto oposto / hipotenusa
seno 30° = OA' / OB
seno 30° = a / √3
1/2 = a / √3
(1/2) x √3 = a
a = (√3)/2 (mesmo valor encontrado anteriormente)
Aproveite e continue praticando com uma lista de questões anteriores da Seeduc-RJ.
Um forte abraço e bons estudos.