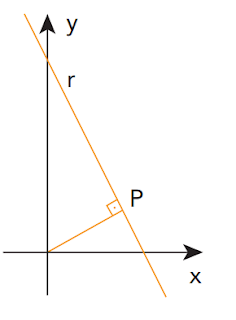
(UERJ 2023) Observe no plano cartesiano a seguir a reta r, de equação y = 5 - 3x, sendo x ∈ R, e seu ponto P, que é o mais próximo da origem.

O ponto P tem a seguinte abscissa: 

(A) 1,3 (B) 1,5 (C) 1,7 (D) 1,9

Solução: questão de matemática do Vestibular UERJ 2023, prova do dia 04/12/2022.

Uma questão bem interessante de geometria analítica, que aborda alguns conceitos ligados a equações de reta.  O objetivo da questão é encontrar a abscissa do ponto P, para fazer isso, vamos criar a reta s, que passa pela origem (0,0) e por P(x,y) conforme a ilustração a seguir:

Agora, vamos obter a equação da reta s, sabemos que a reta s tem equação y = ax + b

O coeficiente b é igual a 0, isto porque a reta s corta o eixo y exatamente na origem, ponto de coordenadas (0,0), logo, sabemos que b = 0 e a equação de s é basicamente do tipo y = ax

Agora, só precisamos obter o coeficiente angular (a) da reta s.  Note que as retas r e s são perpendiculares, logo o produto de seus coeficientes angulares é igual a -1.  Equacionando, temos que

(ms) x (mr) = -1   (equação I)

  • ms é o coeficiente angular da reta s, que é o valor a que queremos descobrir; 
  • mr é o coeficiente angular da reta r, sabemos que mr = -3 , isto porque é o valor do coeficiente que multiplica o x na equação da reta r.    Veja a seguir:  y = 5 - 3x.    

Vamos então aplicar estes valores na equação I para descobrirmos qual é o valor de a:

a . (-3) = -1
-3a = -1
a = 1/3

Sabemos agora que s tem equação y = (1/3).x ou simplesmente y = x/3

Já a reta r tem equação y = 5 - 3x

Finalmente, para encontrar a abscissa do ponto P, que é o ponto de encontro das retas s e r, basta igualarmos as duas equações

x/3 = 5 - 3x
x/3 + 3x = 5
x/3 + 9x/3 = 5
10x/3 = 5
10x = 15
x = 1,5

Alternativa correta é a letra b).

Aproveite e continue praticando com uma lista de questões de matemática da UERJ.

Um forte abraço e bons estudos.