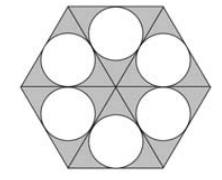
(EEAR CFS 1/2024) Seja um hexágono regular de 2 cm de lado. Ele foi dividido em 6 triângulos equiláteros e, em cada triângulo, foi inscrito um círculo, como na figura. 

Considerando π = 3 e √3 = 1,7 ,  a parte do hexágono que é externa aos círculos tem ______ cm² de área.

a) 3,2 b) 3,6 c) 4,2 d) 4,6

Solução: questão de matemática da EEAR (Escola de Especialistas da Aeronáutica) do Exame de Admissão ao Curso de Formação de Sargentos da Aeronáutica CFS 1/2024. Prova aplicada no dia 04/06/2023.

Repare que a área do hexágono que é externa aos círculos, a qual chamaremos de área objetivo Ao, é igual a seis vezes a área do triângulo equilátero At menos a área do círculo Ac.  Vamos equacionar isso:

Ao = 6 x (At - Ac)     "Equação principal"

O que vamos fazer agora é calcular individualmente a área do triângulo equilátero e a área do círculo inscrito nele.

>> Cálculo de At

Área do triângulo equilátero de lado L pode ser calculada por meio da fórmula

At = (L² . √3)/4

Caso necessário, faça uma revisão sobre como calcular a área de um triângulo equilátero.

Aplicando L = 2 cm na fórmula, encontraremos

At = (2² . √3)/4
At = (4 . √3)/4
At = √3 
Aplicando √3 = 1,7
At = 1,7 cm²

>> Cálculo da Área do Círculo Ac 

Ac = π . R²
Aplicando π = 3
Ac = 3 R²

R é a medida do raio do círculo inscrito no triângulo equilátero, que é igual a 1/3 da altura do triângulo equilátero (caso necessário, revise por aqui).  A altura de um triângulo equilátero de lado L é igual a (L√3)/2 . Deste modo, 

R = (1/3) . (L√3)/2
R = (L√3)/6

Aplicando L = 2cm, encontraremos R

R = (2√3)/6
R = (√3)/3

Finalmente, temos que a área do círculo será 

Ac = 3 . R²
Ac = 3 . [(√3)/3]²
Ac = 3 . (3/9)
Ac = 1 cm²

Finalmente, basta aplicar estes valores na equação principal

Ao = 6 x (At - Ac)
Ao = 6 x (1,7 - 1)
Ao = 6 x (0,7)
Ao = 4,2 cm²

Alternativa correta é a letra c).

Aproveite e continue praticando com uma lista de questões anteriores da EEAR. 

Um forte abraço e bons estudos.