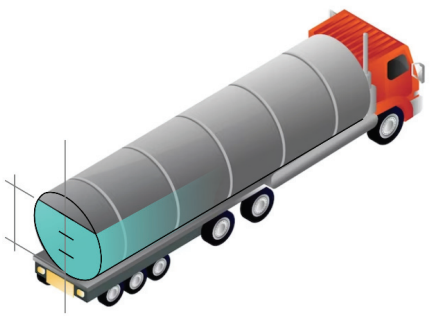
(FUVEST 2024) O reservatório de um caminhão-pipa tem a forma de um cilindro circular reto com eixo horizontal e dimensões internas de 6 metros de comprimento e 2 metros de diâmetro. Uma escola contratou o serviço do caminhão-pipa para abastecer sua caixa d’água. Após o abastecimento, o motorista percebeu que o reservatório do caminhão estava cheio até 3/4 de sua altura, conforme ilustrado na figura.

Qual foi o volume, em metros cúbicos, de água utilizada para abastecer a caixa d’água da escola, sabendo que o reservatório do caminhão estava cheio antes do abastecimento?

a) (2π -  √3  )
                    4

b) (2π -  3√3  )
                    2

c) (2π +  3√3  )
                     2

d) (4π +  √3  )
                     4

e) (4π +  3√3  )
                       2

Solução: questão de matemática da Prova de Conhecimentos Gerais - FUVEST 2024, prova aplicada no dia 19/11/2023.

Uma questão muito interessante de geometria plana e geometria espacial.  Antes de obtermos o volume utilizado nesse abastecimento, podemos notar que o volume total do reservatório é de 6 π m³.  Basta aplicar os valores do enunciado na fórmula do volume do cilindro πR²h.

Observando este reservatório, é notório que o volume referente à altura que vai da marcação de 3/4 até 4/4, é menor que 1,5 π m³.  Isto porque este volume é igual ao volume referente à altura desde a marcação 0 até 1/4.  O volume referente a estes dois intervalos juntos é menor do que o volume que vai da marcação de 1/4 até 3/4.  

Observe atentamente a figura, perceba que o intervalo intermediário (da marcação de 1/4 até 3/4) tem volume superior à soma dos volumes dos extremos.


Vamos fazer uma breve suposição, vamos assumir que o volume referente à altura que vai de 3/4 até 4/4 é de exatamente 1,5 π m³.  Isto obriga o volume que vai de 0 até 1/4 ser também de 1,5 π m³.  Sobrariam outros 3 π m³ para a parte central que vai de 1/4 até 3/4, ou seja, a marcação de 1/4 até 2/4 seria de 1,5 π m³ e a marcação de 2/4 até 3/4 também teria um volume de 1,5 π m³.  Repare visualmente na figura que isso não faz sentido, pois as parcelas intermediárias possuem volumes bem maiores.  Isto quer dizer que podemos garantir pelo desenho da figura que o volume desse abastecimento é inferior a 1,5 π m³.

Com essa breve análise, já podemos eliminar as alternativas (c), (d) e (e), pois elas nos indicam que o volume é sempre maior que 2π m³, o que não faz sentido.  

Ficamos apenas com as alternativas (a) e (b), e devido aos seus respectivos valores,  temos que eliminar também a letra (a), ficando apenas com a letra (b) como opção correta.   Veja o cálculo a seguir utilizando 1,7 como aproximação para √3 :

a) 2π - 1,7/4 ≅ 2π - 0,4  

Sabemos que π ≅ 3,14 de modo que 0,4 é um valor compreendido entre 0,1 π e 0,2 π.  É notório que 2π menos qualquer um desses dois valores será maior do que 1,5 π .  Portanto, eliminamos a letra (a) e a única que pode ser a correta é a letra (b).
 
A seguir, vamos encontrar o valor exato deste volume.  Sabendo que o reservatório do caminhão estava cheio antes do abastecimento, o volume, em metros cúbicos, de água utilizada para abastecer a caixa d’água da escola, pode ser encontrado por meio do produto da área do segmento circular destacado em vermelho, multiplicado por 6 m, vide ilustração.



A seguir, vamos ilustrar esse círculo, um setor circular, um triângulo isósceles e o segmento circular para calcularmos sua área.


Sendo C o centro do círculo, podemos notar que o triângulo CAB é um triângulo isósceles, deste modo, o segmento CD, que vale 0,5 m, é altura, bissetriz e mediana relativa à base AB.  Com estas informações, podemos obter quanto vale o ângulo α utilizando as relações trigonométricas no triângulo retângulo ADC.

cos α = (cateto adjacente)/(hipotenusa)
cos α = CD/AC
cos α = 0,5/1
cos α = 1/2

Sabemos que 0° < α < 90° , isto quer dizer que α = 60°.

O ângulo central do setor circular CAB vale o dobro de α, ou seja, vale 120°.  Vamos atualizar a figura com essa informação e calcular a área do segmento circular.



Área do segmento circular = (Área do setor CAB) - (Área do triângulo CAB)

Área do setor com ângulo central de 120° e raio igual a 1 m equivale a 1/3 da área de um círculo de raio igual a 1 m:

(1/3) . πR²
(1/3) . π.1²
π/3 m²

Área do triângulo CAB pode ser calculada utilizando a fórmula a seguir:

Área = L1 x L2 x sen θ x (1/2)

Sendo, L1 e L2 as medidas de dois lados desse triângulo e θ o ângulo entre esses dois lados.

Área = 1 x 1 x sen 120° x (1/2)

sen 120° = sen 60° = (√3)/2

Área = [(√3)/2] x (1/2)
Área = (√3)/4 m²

Finalmente, temos que 

Área do segmento circular = [(π/3)  - (√3)/4] m²

O volume, em metros cúbicos, de água utilizada para abastecer a caixa d’água da escola, sabendo que o reservatório do caminhão estava cheio antes do abastecimento é igual a área do segmento circular vezes 6 metros.

[(π/3)  - (√3)/4] m²  x  6 m
[(6π/3)  - (6√3)/4] m³
( 2π  - 3√3 ) m³
                   2          
 
Alternativa correta é a letra b).

Aproveite e continue praticando com uma lista de questões de matemática da FUVEST.

Um forte abraço e bons estudos.